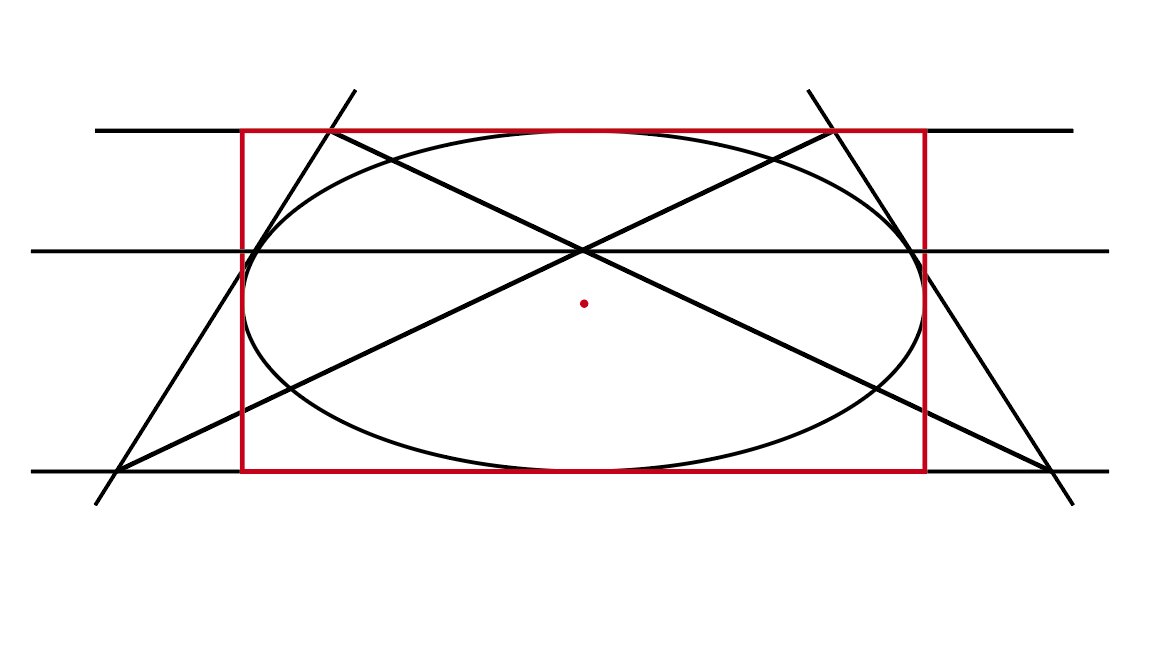
デッサンにおける楕円の問題を解決した図が話題に「円にパースをかけると正楕円になる」

デッサンにおける楕円の問題は端的にこの図によって言い尽くせるかもしれない。 https://t.co/UqgteUcqV2

2022.03.13 17:47:41

@nas740 概念的には図の通りですが、結局歪みのない正楕円でいいんですよね…。

2022.03.13 20:45:39

@zuntok というかまさに歪みのない正楕円でいいという図になります。パースペクティヴ上の中心が奥にズレることで分からなくなりがちな正楕円でいいんだということを明確に言い切るという。

2022.03.13 21:08:00

@nas740 そうですね、僕の書き方が良くなかったです、、。楕円においてはパースのついた正方形と共に歪ませ、間違って説明されてる教則本、多いです。

2022.03.13 21:14:32

@zuntok 実は恥ずかしながら自分もそこがよくわかってなかったのです。正楕円だって言い切ったうえでパース上の中心点を貫く水平の線からしたら歪んでいるともいえるという二重性を説明しないといけないんですよね。

2022.03.13 21:26:03

@nas740 僕もよくわかっておらず、生徒さんには巨大なものを敢えてデフォルメするのでなければ正楕円でいいです、くらいの説明しかしてませんでした。図のような一焦点パースでもややこしいのに、二焦点パース上の歪んだ正方形に内接する楕円だと、シンプルな正楕円なのに図の説明が更にややこしくなりますね。

2022.03.13 22:08:13

@zuntok つまりひとこと「正楕円でいい」というのが一番合理的という説もありますね（笑）

2022.03.13 22:26:57

@nas740 はい。結局それが一番確実に伝わります笑

2022.03.13 22:32:18

@zuntok @nas740 横からすみません。
歪むための進行方向が、かならず円の線上にあるため、見かけ上歪まないということかなと思いました。
そのため、点で描かれた円を斜めから見るとき、手前は間隔が広がり、奥は間隔が詰まります。 https://t.co/CpCNPPc26u

2022.03.14 18:05:38

@Minimumlife_Pro @nas740 そうですね。見かけ状。ピザのように等分にしてもそうですね。ピザ一切れは目からの距離が遠ければより大きく縮みます。楕円の奥のカーブは浅くなり手前は膨らむ事になりますが、元図のようにみかけの中心が奥にずれる事で結果的にアウトラインは正楕円のままという事になります。

2022.03.14 18:24:56

画像を保存しました･･･ t.co/KztayJTbCX

2022.03.14 23:43:43

馬車の車輪とか斜めから書くときいつもラフではパース付き四角で線を整えるときに「？」を浮かべながら正楕円を描いてたけどこういうことだったのか。
t.co/kZXUYoPqoV

2022.03.14 23:43:34

Live2D で直感的にやると楕円回転がへにょる問題と同じやつじゃん t.co/kekkAB1uXW

2022.03.14 23:15:46

赤=平面図の図心.
黒=幾何学遠近図の交点.
他=等角投影図の中心点.
他=製図に於ける重心. t.co/hCbArPRPH3

2022.03.14 22:03:38

図形的な円心とパース的な円心って全然違う場所にあるからここ間違ったら円が死ぬ t.co/9eRgL9AsUT

2022.03.14 21:53:30